Fibered Sumの構成における「同値関係」

代数トポロジーをやってると、adjunction spaceとかmapping torusなんてものにおめにかかるけれど、実はこれらはともに、圏論の概念であるところのfibered sumの特別な場合であるといえる。

僕が過去に読んだ[Mac]*1とか[Str]*2
とかには、圏 $\b{Sets}$ ではfibered sumは必ず存在するとされているのだけれど、その構成に甚だ納得がいかない。
同値関係を入れて、その商集合としてfibered sumを定義しているのだけれど、その関係が、そもそも同値関係になるのか？ということに疑問を抱いた。

そこで、何故納得がいかないのか、ということをまとめた上で、でも納得いかなくてもそれなりに正当化できるんだよ、ということを書いてみようと思いました。
動機は圏論だけれど、記事の内容は集合論。

fibered sumについては次が詳しい。本家wikipedia先生、まじパネェっす。
Pushout (category theory) - Wikipedia, the free encyclopedia

$\b{Sets}$ 上でのfibered sumの「定義」とされるものへの不平不満

さて、既に知られた事実として、 $\b{Sets}$ には常にfibered sumが存在する。
[Str]によると

（前略）define the equivalence relation $\sim$ on $A_1\amalg A_2$ by $a_1\sim a_2$ ( $a_1\in A_1$ and $a_2\in A_2$ ) if and only if there is an element $c\in C$ such that $a_1=f_1(c)$ and $a_2=f_2(c)$ . Then $A_1\amalg_C A_2=A_1\amalg A_2/\sim$ .

一見良さそうに見えるが、問題は、こうして定義された $\sim$ が、本当に同値関係になるのか、ということ。

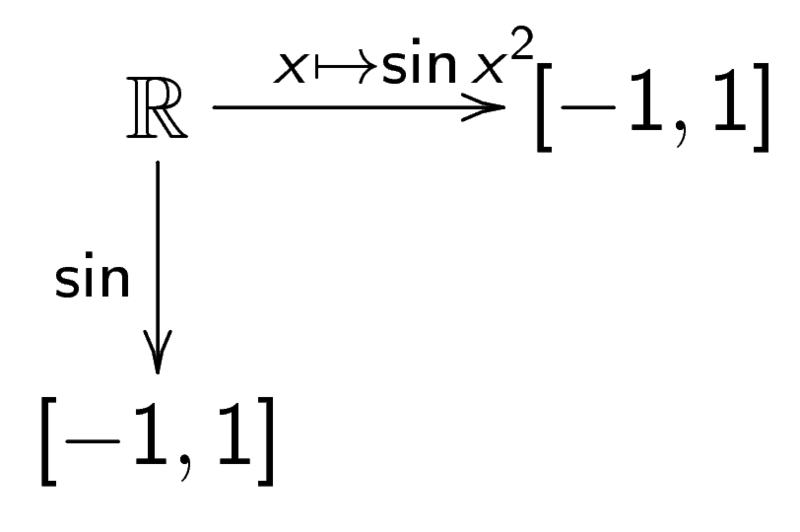
これが以外と難しい問題で、例えば、右の例を考えてみる。
上の同値関係によれば、 $\pi$ の像として
$\sin \pi^2\sim 0$
一方、 $\sin \pi^2=\sin \sqrt{\pi^2+2\pi}^2$ なので、 $\sqrt{\pi^2+2\pi}$ の像として
$\sin \pi^2\sim\sin\sqrt{\pi^2+2\pi}$
でもある。
さらにさらに、 $\sin\sqrt{\pi^2+2\pi}=\sin\left(\sqrt{\pi^2+2\pi}+2\pi\right)$ でもあるので、
$\sin\left(\sqrt{\pi^2+2\pi}+2\pi\right)^2\sim\sin\sqrt{\pi^2+2\pi}$
になってしまう。
すると、推移律によって $\sin\left(\sqrt{\pi^2+2\pi}+2\pi\right)^2\sim 0$ が得られるが、両者が共通の元の像でないことは明らかである。
つまり、[Str]では "if and only if" なんて書いてあるけれど、この関係 $\sim$ が同値関係になるためには、そんなに生易しい定義ではダメなのだ。

一般の2項関係から同値関係を生成する

上で定義した $\sim$ は、そのままでは同値関係ではないということがわかった。
しかし、それ自身は同値関係にならなくとも、その関係によって「生成」された同値関係というものが存在すれば良い。
すなわち、同値関係 $\approx$ があって
$a_1\sim a_2\Rightarrow a_1\approx a_2$
とでき、かつ、 $a_1\sim a_2\Rightarrow a_1\approx' a_2$ であるような同値関係 $\approx'$ についても
$a\approx b\Rightarrow a\approx' b$
が成立するようにできるならば、 $\approx$ は $\sim$ によって生成された同値関係と呼ぶべきものであろう。
そして、 $\sim$ を $\approx$ で置きかえれば、[Str]の議論は正しかろうと予想される。

命題
$A$ を集合、 $\sim$ をその上の任意の2項関係とする。
この時、同値関係 $\approx$ で、次を満たすものが存在する。

$a\sim b\Rightarrow a\approx b$

$A$ 上の同値関係 $R$ で $a\sim b\Rightarrow aRb$ ならば、 $a\approx b\Rightarrow aRb$

（証明）
$\cal{R}_{\sim}$ を $A$ 上の同値関係 $R$ で、
$a\sim b\Rightarrow aRb$
が成立するもの全体とする。
この時、 $A$ 上の関係 $\approx$ を次で定義する。
$a\approx b\,\Leftrightarrow\,\forall R\in\cal{R}_{\sim}\,:\,aRb$
まず、 $\approx$ は同値関係である。
実際、 $\forall R\in\cal{R}_{\sim}$ が反射率、対称律、推移律を満たしているので、 $\approx$ もそれらを満たすはずである。

$\cal{R}_{\sim}$ と $\approx$ の定義から、
$a\sim b\,\Rightarrow\,\forall R\in\cal{R}_{\sim},:\,aRb\,\Rightarrow\,a\approx b$
である。
また、 $a\sim b\Rightarrow aRb$ であるような $A$ 上の同値関係 $R$ は $R\in\cal{R}_{\sim}$ なので、 $\approx$ の定義から、
$a\approx b\Rightarrow aRb$
が成立する。
以上より、 $\approx$ が求める同値関係である。
（証明終）
すごい豪快な作り方だけれど、存在は確認できた。
さらに、2番目の条件から、このような同値関係は唯一つであることもわかる。

「生成」した同値関係でfibered sum

それでは、上で存在性を示した $\approx$ によって、 $\b{Sets}$ におけるfibered sumを構成する。

命題
$f_1:A\to X_1,f_2:A\to X_2$ を $\b{Sets}$ における射とする。
この時、 $\approx$ を $f_1(a)\approx f_2(a)$ によって生成される $X_1\amalg X_2$ 上の同値関係とする。
この時、 $X=X_1\amalg X_2/\approx$ とし、 $i_1:X_1\to X,i_2:X_2\to X$ をそれぞれ包含写像 $\tilde{i}_1,\tilde{i}_2$ と商写像 $q$ の合成とすると、 $X=X_1\amalg_A X_2$ である。

（証明）

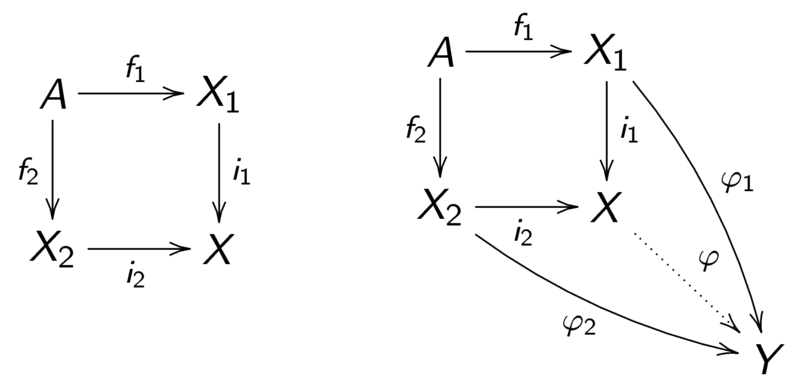
上左図が可換であることは、同値関係の定義から従う。
今、 $\varphi_1:X_1\to Y,\varphi_2:X_2\to Y$ は上右図を可換にするものとする。
この時、 $\varphi_1,\varphi_2$ によって $\tilde{\varphi}:X_1\amalg X_2\to Y$ があり、 $\varphi_1=\tilde{\varphi}\circ\tilde{i}_1,\varphi_2=\tilde{\varphi}\circ\tilde{i}_2$ とできる。
これを用いて、 $\varphi:X\to Y$ を次で定める（右図）。
$\varphi([x]):=\tilde{\varphi}(x)$
この写像はwell-definedである。
実際、 $X_1\amalg X_2$ 上の関係
$xRx'\Leftrightarrow \tilde{\varphi}(x)=\tilde{\varphi}(x')$
は同値関係であり、さらに図の可換性より、各 $a\in A$ で $f_1(a)Rf_2(a)$ であるから、 $\approx$ の定義より
$x\approx x'\Rightarrow xRx' \Rightarrow \tilde{\varphi}(x)=\tilde{\varphi}(x')$
が言える。
さらに、図式より
$\varphi_1=\tilde{\varphi}\circ\tilde{i}_1=\varphi\circ q\circ\tilde{i}_1=\varphi\circ i_1$
同様に、 $\varphi_2=\varphi\circ i_2$ も成立するので、よって、 $(X,i_1,i_2)$ はuniversal propertyを満たす。
（証明終）

なるほど、「生成する」という考え方がこのように生きてくるのか。
しかし、このように商を作る際の同値関係が不明瞭なままでは、fibered sumの存在性は言えても、その構成を用いた議論が難しくなってしまうのではないだろうか。
特にトポロジーの本は、圏論をメインに扱っている訳ではないので、空間の性質を全て圏論の言葉に翻訳するなんてことはしないはずで、そうすると、構成そのものが重要になってくる場合も多いのでは？

*1:[Mac] S.MacLane, Categories for the working mathematician, Springer 1971 [asin:0387984038:detail]

*2:[Str] J.R.Strooker, Introduction to categories, homological algebra and sheaf cohomology, Cambridge University Press 1978 [asin:0521095255:detail]